

(iii) The Ionic Product of Water
'When a reaction at equilibrium is subject to change the composition alters in such a way as to minimise the effects of that change.
Click here to recap Equilibria from Higher.
A chemical reaction is said to be in equilibrium when -the rate of the forward reaction is equal to the rate of the reverse reaction.
A + B ⇋ C + D
A chemical system in equilibrium shows no change in:
The equilibrium constant (K) characterises the equilibrium composition of the reaction mixture.
For the general reaction:
aA +bB → cC + dD
where [A], [B], [C] and [D] are the equilibrium concentrations of A, B, C and D, respectively, and a, b, c and d are the stoichiometric coefficients in a balanced reaction equation.
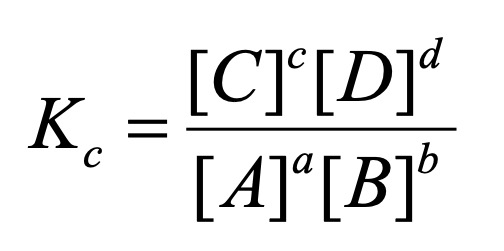
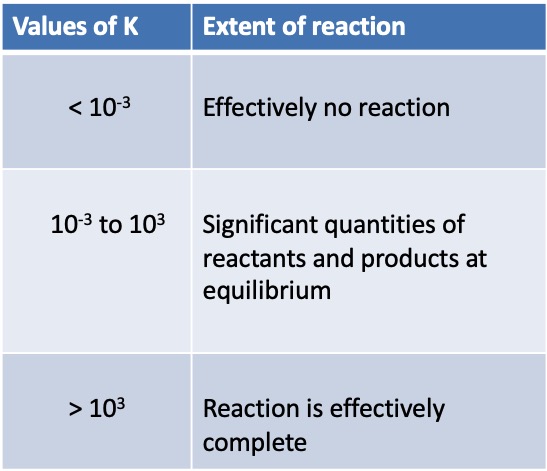
K indicates the ration of products to reactants and therefore has no units.
The equilibrium constant, K, gives no indication of the rate at which equilibrium is achieved.
However, the extent of the reaction can be determined from the constant.
Examples:
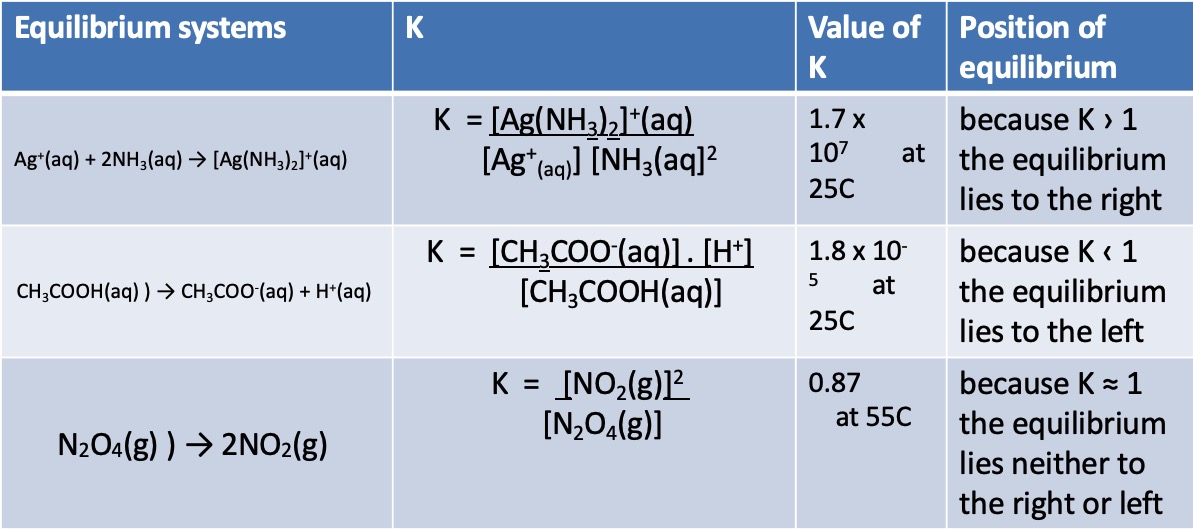
For gas reactions, the pressures of each species ('partial pressures') in the reaction mixture can be used in the same way as concentration.
Remember, K is constant at any given temperature.
In the Haber process...
H2(g) + N2(g) ⇋ 2NH3(g)
The K is fixed,
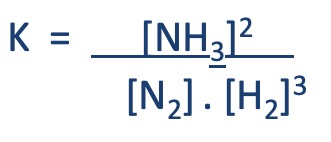
In the following examples, although the position of equilibrium has changed, the value of K has not.
Example 1
If NH3 is removed, the equilibrium position moves to the right, more NH3 is produced.
N2 and H2 are effectively removed as they react and so the value of K is unaltered.
Example 2
If N2 is added, the equilibrium moves to the right, more NH3 is produced and again the value of K is unaltered.
In both examples, although the position of equilibrium has changed, the value of K has not.
The Haber process is an example of Homogeneous Equilibrium. All the species are in the same phase.
In a Heterogeneous Equilibrium the reactants and products are in more than one phase.
When a liquid or solid is present in the reaction, its 'concentration' is effectively constant and given a value of 1.
For example,
CaCO3(s) ⇋ CaO(s) CO2(g)
K = CO2
At any given temperature K is constant.
The equilibrium constant, K, for a reaction is dependant on temperature.
In an Exothermic reaction K decreases with temperature increase, i.e. yield decreases,
In an Endothermic reaction K increases with temperature increase i.e. yield increases.
This is because, when the temperature of an equilibrium system is increased, the rates of both the forward and reverse reactions increase but not by the same value because their activation energies are different.
For example,
H2(g) + N2(g) ⇋ 2NH3(g) ΔH = -46 KJmol-1
In this example, the system has an exothermic forward reaction. A rise in temperature therefore favours the reverse (endothermic) reaction. This leads to a decrease in the value of the equilibrium constant, K, as the equilibrium position moves to the left.
Catalysts do NOT affect Equilibrium position as they lower the activation energy of both the forward and reverse reactions to the same extent.
If a solute is added to two different solvents, it is likely to be more soluble in one than in the other.
If these two solvents are immiscible liquids (do not mix), then the solute will distribute itself between the two liquids in a different ratio, called the partition coefficient.
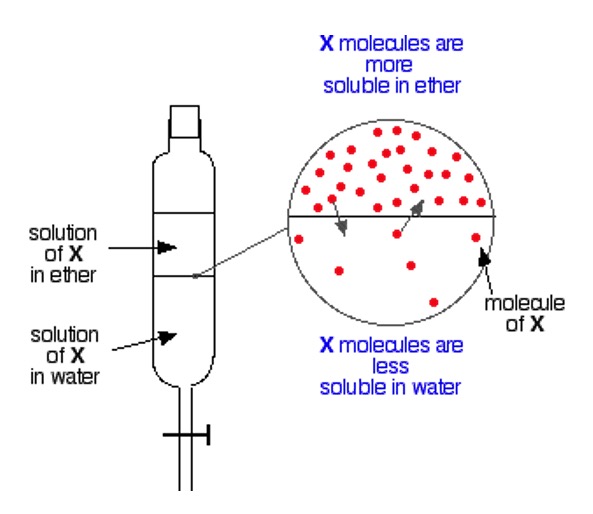
The solute has dissolved into each solvent in a specific ratio named 'The partition coefficient'.
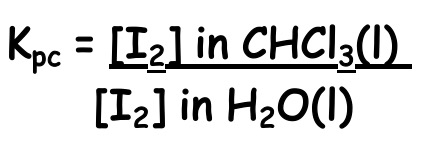
The value of the partition coefficient depends on the immiscible liquids and solute used and (in common with all equilibria), the temperature.
Organic compounds are normally more soluble in non-polar solvents, such as methylbenzene (toluene), trichloromethane (chloroform) or ethoxyethane (diethyether) than they are in water.
Less is More
It is more efficient to use small quantities of non polar solvent in repeated extractions than a single extraction with a large volume of non polar solvent.
One extraction using 100ml of ether will give a lower extraction yield than 2 extractions of 50ml each.
You were taught in National 5 Chemistry that the water molecule is in equilibrium with the hydrogen and hydroxide ions.
H2O(l) ⇋ H+(aq) + OH-(aq)
However...
A hydrogen ion is basically a proton (hydrogen atom that has lost an electron) and only exists when surrounded by water molecules in an aqueous solution. These are known as hydronium ions and are written as H3O+(aq) but are often shortened to just H+(aq).
2H2O(l) ⇋ H3O+(aq) + OH-(aq)
Water is said to be amphoteric. It can act as an acid as or a base.
H2O(l)(acid) + H2O(l)(base) ⇋ H3O+(aq) + OH-(aq)
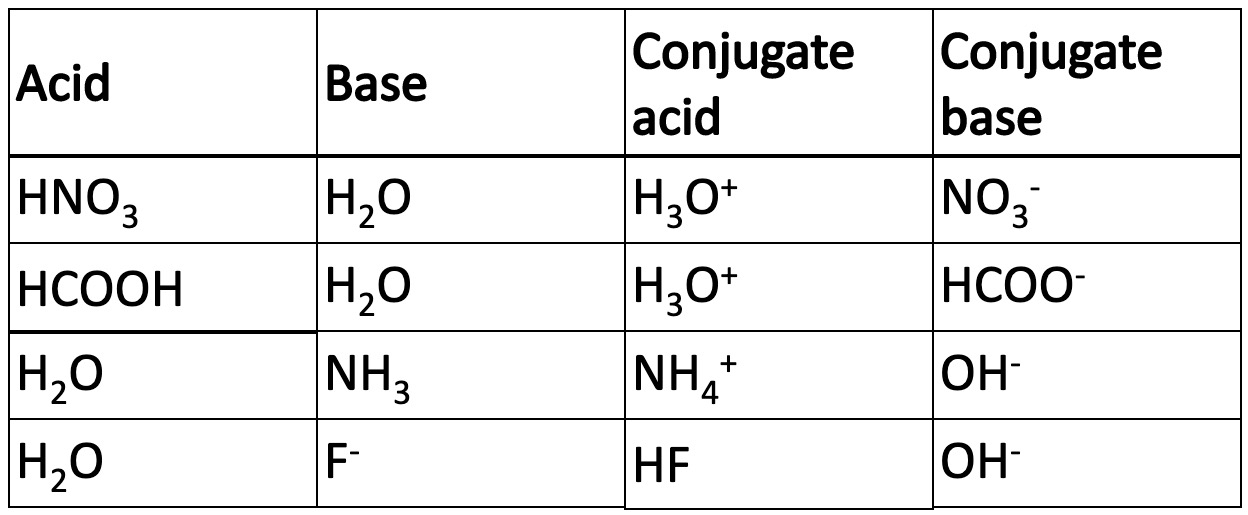
An acid therefore is a proton donor and a base is a proton acceptor. This definition was put forward by Bronsted and Lowry in 1932.
When an acid donates a proton the species left is called the conjugate base.
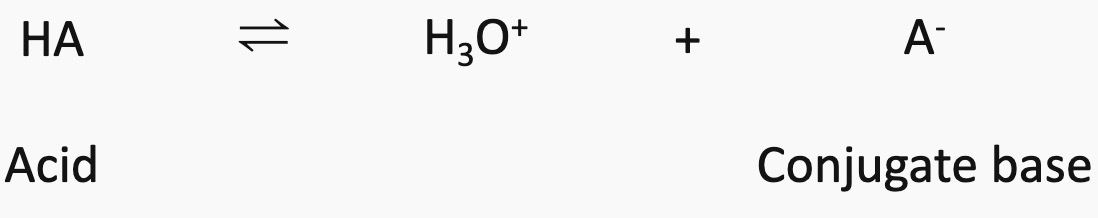
When a base accepts a proton the species formed is a conjugate acid.
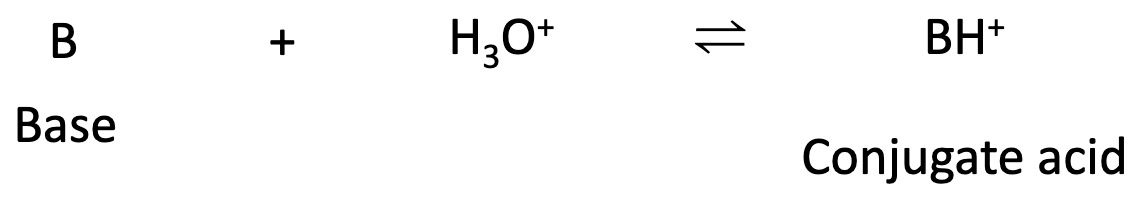
In the examples in the table below water acts as an acid and a base.
An equilibrium is reached when [H3O+] = [OH-] = 1 x 10-7 mol l-1 @ 25oC.
Kw= [H3O+] [OH-]
[H+] [OH-] = 1 x 10-7 mol l-1 x 1 x 10-7 mol l-1
[H+] [OH-] = 1 x 10-14 mol2l-2
Kw = [H+] [OH-] = 1 x 10-14
This can be used to calculate [H3O+], pH and [OH-]
The concentration of hydrogen ions in a solution is measured in pH units.
pH stands for the negative logarithm (to base 10) of the hydrogen ion concentration.
pH or hydrogen ion concentration can be calculated by:
pH = -log10[H3O+(aq)] or [H3O+(aq)] = 10-pH
These equations can be found in the front page of your databook.
Calculate the concentration of OH- ions in a solution containing 0.01 moll-1 of H3O+ ions.
Calculate the pH of a solution that contains 0.01 moll-1 of H3O+ ions
Calculate [H3O+] from a pH value of 11.6.
Calculate the pH of a solution of 0.006 mol l-1 sodium hydroxide.
Strong acids and bases are those that completely dissociate when dissolved in water
| Strong Acids | Strong Bases |
|---|---|
| Hydrochloric acid | Sodium hydroxide |
| Nitric acid | Potassium hydroxide |
| Sulphuric acid | Barium hydroxide |
e.g.
HCl(aq) → H+(aq) + Cl-(aq)
NaOH(aq) → Na+(aq) + OH-(aq)
Weak acids and bases do not fully dissociate into ions.
| Weak Acids | Weak Bases |
|---|---|
| Ethanoic Acid | Ammonia |
| Citric Acid | Amine Solutions |
| malic acid |
e.g.
CH3COOH(aq) ⇋ CH3COO-(aq) + H+(aq)
The pH of salts is often not 7.
In general terms, in solution:
In the 19th century, Swedish chemist, Svante August Arrhenius defined acids as producing hydrogen ions in solution and bases as producing hydroxide ions in solution.
It was Arrhenius who suggested that strong acids dissociated (broke up into their ions) completely in aqueous solution, e.g.
HCl → H++ Cl-
and that weak acids dissociated (broke up into their ions) incompletely in which most of the molecules remaining in the undissociated form, e.g.
CH3COOH → CH3COO- + H+
For a strong monoprotic acid such as HCl or HNO3, the hydrogen ion concentration is the same as the concentration of the acid.
e.g. In 0.1 mol l-1 HCl(aq), [H+] = 0.1 mol l-1
However for weak acids that are only partially dissociated, less than 5% of the acid particles become ions in water.
Therefore, we need a different method to calculate the [H+] and pH for an aqueous solution of a weak acid.
For the dissociation of a weak acid HA,
HA ⇋ H+ + A-
Ka = [H+] [A-] / [HA]
The value of Ka gives a measure of the strength of an acid. The Ka values for acids can be found on p13 0f the Data Book.
Since Ka gives a measure of the degree of dissociation of a weak acid, it can be used to allow us to calculate the pH for a weak acid solution.
Ar equlibrium,
[H+] = [A-]
Therefore,
Ka = [H+]2 / [HA]
as c = [HA],
Ka = [H+]2 / c
Rearanged to give,
[H+]2 = Ka c
and,
[H+] = √ Ka c
Since,
pH = -log[H+]
pH = -log√ Ka c
As,
-logKa = pKa and pH = -1/2logKa - 1/2logc
The equation then becomes,
pH = 1/2pKa - 1/2logc
Hence, the larger the Ka value the stronger the acid and the smaller the pKa value the stronger the acid.
Indicators are weak acids which have a different colour to their conjugate base.
HIn(aq) ⇋ H+(aq) + In-(aq)
low pH: equilibrium pushed left = colour 1
high pH: equilibrium pushed right = colour 2
Kin = [H+][In- ] / [HIn]
-log KIn = -log [H+] - log [In-] / [HIn]
Since,
pKIn= -logKIn and, pH = -log[H+]
Then,
pKIn = pH - log [In- ] / [HIn]
pH = pKIn + log [In- ] / [HIn]
Therefore, the overall pH of the solution is given by the pKIn and the negative log of [In-] over [HIn].
As the In- ion and HIn are different colours, the negative log of [In-] over [HIn] determines the colour of the solution.
To be able to distinguish a colour change [In-] and [HIn] need to differ by a factor of ten. The pH range for the colour change can be estimated by the formula pKIn ± 1. This can be found on page 4 of the databook.
When an acid is neutralised by a base there is a very rapid change in pH around the equivalence point. The equivalence point is the point at which the exact amount of base has been added to neutralise the acid.
pH can be monitored during a titration using a pH meter. The equivalence point can clearly be seen when a graph is plotted of the pH against volume.
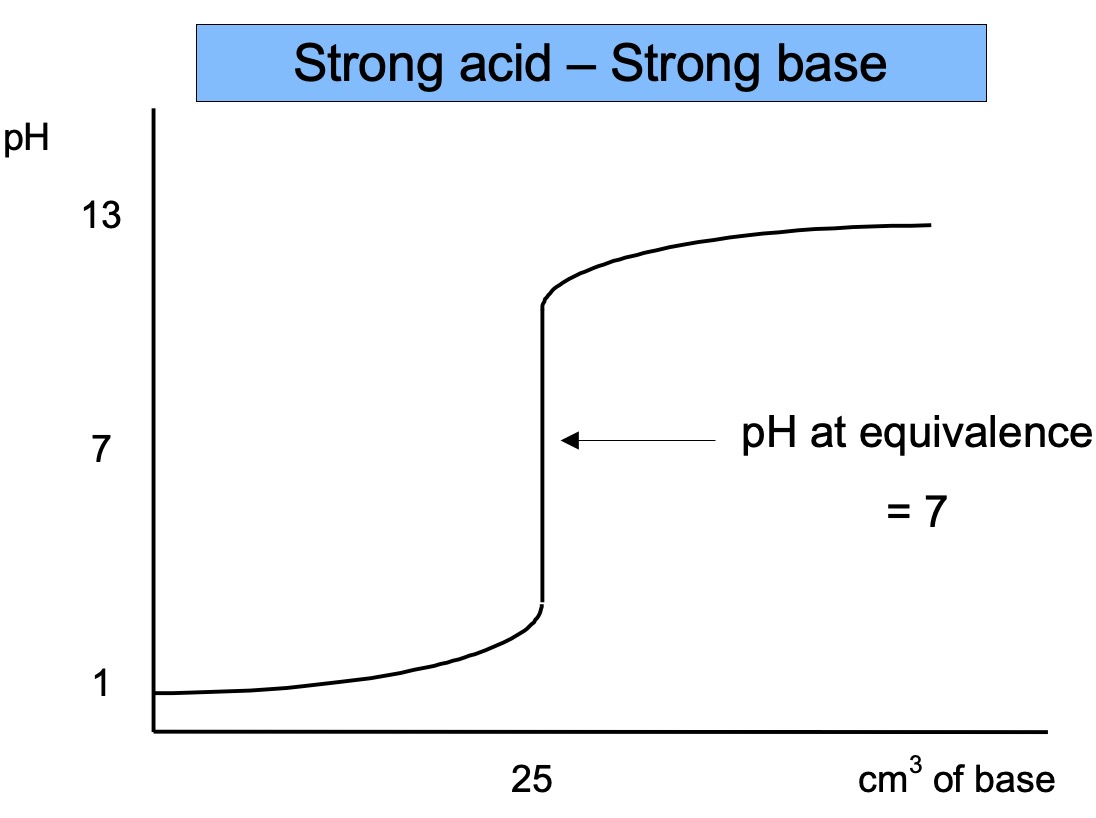
The equivalence point occurs at different pHs when different combinations of strong and weak acids and bases are used.
When deciding on a suitable indicator the equivalence point should fall within the range of the indicator.
The table below shows the ranges of some common indicators.
| Indicator | colour at low pH | pH range of colour change | colour at high pH |
|---|---|---|---|
| methyl orange | red | 3.2-4.4 | orange |
| phenolphthalein | colourless | 8.2-10 | purple |
The pH ranges of other indicators can be found on page 14 of your data book.
A buffer solution is one in which the pH remains relatively constant with small additions of acid or alkali.
Buffer solutions are particularly important in biological systems. For example, the pH of blood must remain with a pH range of 7.35 - 7.45. Changes outwith this range can be fatal.
There are two types of buffer solution, one between a weak acid and one of its salts and one between a weak base and one of its salts.
example one - Acid added to water:
| Volume of acid solution (cm3) | 0 | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|---|
| pH | 7.0 | 2.7 | 2.4 | 2.2 | 2.1 | 2.0 |
There is a large initial drop in pH particularly around the first addition.
example 2 - the same volume of acid added to a buffer solution:
| Volume of acid solution (cm3) | 0 | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|---|
| pH | 5.07 | 5.06 | 5.05 | 5.02 | 5.01 | 5.00 |
In this example the weakly acidic solution resists further decrease in pH on addition of acid.
An acid buffer is a solution in which a salt of a weak acid is dissolved in the weak acid. The hydrogen ions from the acid will slightly dissociate whereas the ions from the salt will fully dissociate.
e.g.
HA ⇋ H3O+ + A-
The equilibrium position of the weak acid lies to the left. Very few of the hydrogen ions dissociate.
MA → M+ + A-
The equilibrium position of the salt (MA) lies to the right. The salt has fully dissociated into ions.
As there is a large concentration of A- ions in solution they will absorb any hydrogen ions added to the solution by an acid.
Sodium ethanoate acts as a buffer for ethanoic acid.
As ethanoic acid is a weak acid it only partially dissociates into ions. The equilibrium position lies to the left.
CH3COOOH(aq) ⇋ H3O+(aq) + CH3COO-(aq)
In solution, sodium ethanoate separates into ions and the equilibrium lies to the right:
CH3COO-Na+(aq) → Na+(aq) + CH3COO-(aq)
The additional ethanoate ions from the buffer react from the dissociated hydrogen ions from the weak acid and produce more ethanocic acid. The equilibrium shifts back to the left and the pH remains relatively unchanged.
HA ⇋ H+ + A-
Ka = [H+] [A-] / [HA]
[H+] = Ka [HA] / [A-]
-log10[H+] = -log10Ka -log10[HA] / [A-]
As,
-log10[H+] = pH and -log10Ka = pKa
pH = pKa - log10 [HA] / [A-]